Cho Hình Chóp (S.ABCD ) Có đáy (ABCD ) Là Hình Thang Với (AB P

Một sản phẩm của Tuyensinh247.comCho hình chóp (S.ABCD ) có đáy (ABCD ) là hình thang với (AB parallel CD ). Gọi (I ) là giao điểm của (AC ) và (BD ). Trên cạnh (SB ) lấy điểm (M ). Tìm giao tuyến của hai mặt phẳng (( (ADM) ) ) và (( (SAC) ) ).Câu 8301 Vận dụng

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang với \(AB\parallel CD\). Gọi \(I\) là giao điểm của \(AC\) và \(BD\). Trên cạnh \(SB\) lấy điểm \(M\). Tìm giao tuyến của hai mặt phẳng \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\).

Đáp án đúng: b

Phương pháp giải

- Tìm giao điểm dễ thấy của hai mặt phẳng.

- Tìm giao điểm thứ hai bằng cách tìm hai đường thẳng nằm trong hai mặt phẳng mà chúng cắt nhau.

Xem lời giải

Lời giải của GV Vungoi.vn

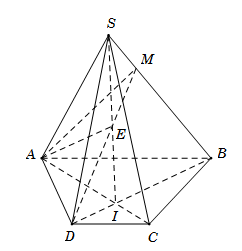
Ta có \(A\) là điểm chung thứ nhất của \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\).

Trong mặt phẳng \(\left( {SBD} \right)\), gọi \(E = SI \cap DM\).

Ta có:

● \(E \in SI\) mà \(SI \subset \left( {SAC} \right)\) suy ra \(E \in \left( {SAC} \right)\).

● \(E \in DM\) mà \(DM \subset \left( {ADM} \right)\) suy ra \(E \in \left( {ADM} \right)\).

Do đó \(E\) là điểm chung thứ hai của \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\).

Vậy $AE$ là giao tuyến của \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\).

Đáp án cần chọn là: b

...

Bài tập có liên quan

Đại cương về đường thẳng và mặt phẳng Luyện Ngay

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi liên quan

Cho $2$ đường thẳng \(a,b\) cắt nhau và không đi qua điểm \(A\). Xác định được nhiều nhất bao nhiêu mặt phẳng bởi $a,b$ và $A$?

Trong các mệnh đề sau mệnh đề nào sai?

Hình nào sau đây vẽ đúng quy tắc?

Một hình không gian có hình chiếu đứng (nhìn từ trước vào (có thể nhìn từ sau) để từ hình 3D chuyển sang hình 2D) hình chiếu bằng (nhìn từ trên xuống) có thể nhìn từ dưới lên)), hình chiếu cạnh (từ trái sang (có thể nhìn từ phải sang)) lần lượt được thể hiện như sau:

Hãy vẽ hình biểu diễn của hình đó?

Cho tứ giác lồi \(ABCD\) và điểm $S$ không thuộc $mp\left( {ABCD} \right)$. Có bao nhiêu mặt phẳng phân biệt xác định bởi $3$ trong số các điểm $A,B,C,D,S$?

Cho bốn điểm không đồng phẳng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân biệt từ bốn điểm đã cho ?

Trong mp\(\left( \alpha \right)\), cho bốn điểm \(A,B,C,D\) trong đó không có ba điểm nào thẳng hàng. Điểm \(S \notin mp\left( \alpha \right)\). Có mấy mặt phẳng tạo bởi \(S\) và hai trong số bốn điểm nói trên?

Trong mặt phẳng \(\left( \alpha \right)\) cho tứ giác \(ABCD\), điểm \(E \notin \left( \alpha \right)\). Hỏi có bao nhiêu mặt phẳng phân biệt tạo bởi ba trong năm điểm \(A,B,C,D,E\)?

Cho năm điểm \(A,B,C,D,E\) trong đó không có bốn điểm nào ở trên cùng một mặt phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong số năm điểm đã cho?

Trong các hình sau:

Các hình có thể là hình biểu diễn của một hình tứ diện là:

Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là :

Trong các hình chóp, hình chóp có ít cạnh nhất có số cạnh là bao nhiêu?

Chọn khẳng định sai trong các khẳng định sau?

Cho hình chóp \(S.ABCD\) có đáy là hình thang \(ABCD{\rm{ }}\left( {AB\parallel CD} \right).\) Khẳng định nào sau đây sai?

Cho tứ diện \(ABCD.\) Gọi \(G\) là trọng tâm của tam giác\(BCD.\) Giao tuyến của mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right)\)là:

Cho điểm $A$ không nằm trên mặt phẳng $\left( \alpha \right)$ chứa tam giác $BCD.$ Lấy $E,\,\,F$ là các điểm lần lượt nằm trên các cạnh $AB,\,\,AC.$ Khi $EF$ và $BC$ cắt nhau tại $I,$ thì $I$ không phải là điểm chung của hai mặt phẳng nào sau đây?

Cho tứ diện \(ABCD.\) Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm của \(AC,{\rm{ }}CD.\) Giao tuyến của hai mặt phẳng \(\left( {MBD} \right)\) và \(\left( {ABN} \right)\) là:

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm \(AD\) và \(BC.\) Giao tuyến của hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right)\) là:

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(I,{\rm{ }}J\) lần lượt là trung điểm \(SA,{\rm{ }}SB.\) Khẳng định nào sau đây sai?

Cho hình chóp \(S.ABCD\) có đáy là hình thang \(ABCD{\rm{ }}\left( {AD\parallel BC} \right).\) Gọi \(M\) là trung điểm \(CD.\) Giao tuyến của hai mặt phẳng \(\left( {MSB} \right)\) và \(\left( {SAC} \right)\) là:

Cho 4 điểm không đồng phẳng $A,\,\,B,\,\,C,\,\,D.$ Gọi $I,\,\,K$ lần lượt là trung điểm của $AD$ và $BC.$ Giao tuyến của $\left( {IBC} \right)$ và $\left( {KAD} \right)$ là:

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang với \(AB\parallel CD\). Gọi \(I\) là giao điểm của \(AC\) và \(BD\). Trên cạnh \(SB\) lấy điểm \(M\). Tìm giao tuyến của hai mặt phẳng \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\).

Cho tứ diện $ABCD$ và điểm $M$ thuộc miền trong của tam giác $ACD\,.$ Gọi $I$ và $J$ lần lượt là hai điểm trên cạnh $BC$ và $BD$ sao cho $IJ$ không song song với $CD\,.$ Gọi $H,\,\,K$ lần lượt là giao điểm của $IJ$ với $CD$, của $MH$ và $AC\,.$ Giao tuyến của hai mặt phẳng $\left( {ACD} \right)$ và $\left( {IJM} \right)$ là: