Giải Bài Tập SGK Giải Tích 12 Nâng Cao: Cực Trị Của Hàm Số
Có thể bạn quan tâm
Bài viết hướng dẫn giải các bài tập trong phần câu hỏi và bài tập và phần luyện tập của sách giáo khoa Giải tích 12 nâng cao: Cực trị của hàm số.
CÂU HỎI VÀ BÀI TẬP
Bài 11. Tìm cực trị của các hàm số sau: a) $f(x) = \frac{1}{3}{x^3} + 2{x^2} + 3x – 1.$ b) $f(x) = \frac{1}{3}{x^3} – {x^2} + 2x – 10.$ c) $f(x) = x + \frac{1}{x}.$ d) $f(x) = |x|(x + 2).$ e) $f(x) = \frac{{{x^5}}}{5} – \frac{{{x^3}}}{3} + 2.$ f) $f(x) = \frac{{{x^2} – 3x + 2}}{{x – 1}}.$
a) Hàm số đã cho xác định trên $R.$ Ta có: $f'(x) = {x^2} + 4x + 3.$ Từ đó $f'(x) = 0$ $ \Leftrightarrow x = – 1$ hoặc $x = – 3.$ Cách 1. Bảng biến thiên:

Vậy hàm số đạt cực đại tại điểm $x = -3$, giá trị cực đại của hàm số là ${f_{CĐ}} = f( – 3) = – 1$, hàm số đạt cực tiểu tại điểm $x = -1$, giá trị cực tiểu của hàm số là ${f_{CT}} = f( – 1) = – \frac{7}{3}.$ Cách 2. $f”(x) = 2x + 4$ $ \Rightarrow f”( – 3) = – 2 < 0$, $f”( – 1) = 2 > 0.$ Vậy hàm số đạt cực đại tại điểm $x = -3$, giá trị cực đại của hàm số là: ${f_{CĐ}} = f( – 3) = – 1$, hàm số đạt cực tiểu tại điểm $x = -1$, ${f_{CT}} = f( – 1) = – \frac{7}{3}.$ b) Tập xác định: $R.$ $f'(x) = {x^2} – 2x + 2$ $ = {(x – 1)^2} + 1 > 0$, $\forall x \in R$ $ \Rightarrow f(x)$ luôn đồng biến nên hàm số không có cực trị. c) Tập xác định: $R\backslash 0\} .$ $f'(x) = 1 – \frac{1}{{{x^2}}}$ $ = \frac{{{x^2} – 1}}{{{x^2}}}$, $f'(x) = 0$ $ \Leftrightarrow x = \pm 1.$ Cách 1. Bảng biến thiên:

Vậy hàm số đạt cực đại tại $x = – 1$, ${f_{CĐ}} = f( – 1) = – 2$, hàm số đạt cực tiểu tại $x = 1$, ${f_{CT}} = f(1) = 2.$ Cách 2. $f”(x) = \frac{{2x}}{{{x^4}}} = \frac{2}{{{x^3}}}.$ Vì $f”(x) = – 2 < 0$ nên hàm số đạt cực đại tại $x = – 1$, ${f_{CĐ}} = f( – 1) = – 2.$ $f”(1) = 2 > 0$ nên hàm số đạt cực tiểu tại $x = 1$, ${f_{CT}} = f(1) = 2.$ d) $f(x)$ xác định và liên tục trên $R.$ Ta có: $f(x) = \left\{ {\begin{array}{*{20}{l}} {x(x + 2)}&{{\rm{với}}\:x \ge 0}\\ { – x(x + 2)}&{{\rm{với}}\:x < 0} \end{array}} \right.$ $ \Rightarrow f'(x) = \left\{ {\begin{array}{*{20}{l}} {2x + 2}&{{\rm{với}}\:x > 0}\\ { – 2x – 2}&{{\rm{với}}\:x < 0} \end{array}} \right..$ Bảng biến thiên:
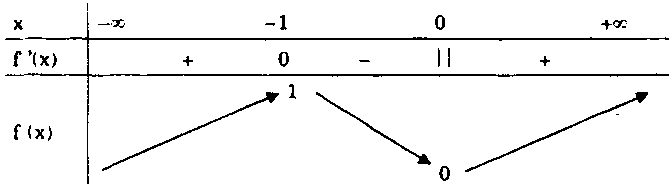
Hàm số đạt cực đại tại $x = – 1$, ${f_{CĐ}} = f( – 1) = 1.$ Hàm số đạt cực tiểu tại $x = 0$, ${f_{CT}} = f(0) = 1.$ e) Tập xác định: $R.$ $f'(x) = {x^4} – {x^2}$, $f'(x) = 0$ $ \Leftrightarrow x = 0$ hoặc $x = \pm 1.$ Bảng biến thiên:

Vậy: Hàm số đạt cực đại tại $x = – 1$, ${f_{CĐ}} = f( – 1) = \frac{{32}}{{15}}.$ Hàm số đạt cực tiểu tại $x = 1$, ${f_{CT}} = f(1) = \frac{{28}}{{15}}.$ f) Tập xác định: $R\backslash \{ 1\} .$ Ta có: $f'(x) = \frac{{(2x – 3)(x – 1) – \left( {{x^2} – 3x + 3} \right)}}{{{{(x – 1)}^2}}}$ $ = \frac{{{x^2} – 2x}}{{{{(x – 1)}^2}}}.$ $f'(x) = 0$ $ \Leftrightarrow x = 0$ hoặc $x = 2.$ Bảng biến thiên:

Vậy: Hàm số đạt cực đại tại $x = 0$, ${f_{CĐ}} = f(0) = – 3.$ Hàm số đạt cực tiểu tại $x = 2$, ${f_{CT}} = f(2) = 1.$
Bài 12. Tìm cực trị của các hàm số sau: a) $y = x\sqrt {4 – {x^2}} .$ b) $y = \sqrt {8 – {x^2}} .$ c) $y = x – \sin 2x + 2.$ d) $y = 3 – 2\cos x – \cos 2x.$
a) Tập xác định: $[ – 2;2].$ $y’ = \sqrt {4 – {x^2}} + x\frac{{ – 2x}}{{2\sqrt {4 – {x^2}} }}$ $ = \frac{{4 – 2{x^2}}}{{\sqrt {4 – {x^2}} }}.$ $y’ = 0$ $ \Leftrightarrow x = \pm \sqrt 2 .$ Bảng biến thiên:

Hàm số đạt cực tiểu tại $x = – \sqrt 2 $, ${y_{CT}} = y( – \sqrt 2 ) = – 2.$ Hàm số đạt cực đại tại $x = \sqrt 2 $, ${y_{CĐ}} = y(\sqrt 2 ) = 2.$ b) Tập xác định: $[ – 2\sqrt 2 ;2\sqrt 2 ].$ $y’ = \frac{{ – x}}{{\sqrt {8 – {x^2}} }}$, $y’ = 0$ $ \Leftrightarrow x = 0.$ Bảng biến thiên:

Vậy: Hàm số đạt cực đại tại $x = 0$, ${y_{CĐ}} = y(0) = 2\sqrt 2 .$ Hàm số không có cực tiểu. c) Tập xác định: $R.$ $y’ = (x – \sin 2x + 2)’$ $ = 1 – 2\cos 2x.$ $y’ = 0$ $ \Leftrightarrow 1 – 2\cos 2x = 0$ $ \Leftrightarrow x = \pm \frac{\pi }{6} + k\pi $, $k \in Z.$ $y” = 4\sin 2x.$ Ta có: $y”\left( {\frac{\pi }{6} + k\pi } \right)$ $ = 4\sin \left( {\frac{\pi }{3} + k2\pi } \right)$ $ = 2\sqrt 3 > 0.$ $y”\left( { – \frac{\pi }{6} + k\pi } \right)$ $ = 4\sin \left( { – \frac{\pi }{3} + k2\pi } \right)$ $ = – 2\sqrt 3 < 0.$ Vậy hàm số đạt cực đại tại các điểm $x = – \frac{\pi }{6} + k\pi $, $k \in Z.$ ${y_{CĐ}} = y\left( {\frac{\pi }{6} + k\pi } \right)$ $ = 2 + \frac{{\sqrt 3 }}{2} – \frac{\pi }{6} + k\pi $, $k \in Z.$ Hàm số đạt cực tiểu tại điểm $x = \frac{\pi }{6} + k\pi $, $k \in Z.$ ${y_{CT}} = y\left( {\frac{\pi }{6} + k\pi } \right)$ $ = 2 – \frac{{\sqrt 3 }}{2} + \frac{\pi }{6} + k\pi $, $k \in Z.$ d) Tập xác định: $R.$ $y’ = 2\sin x + 2\sin 2x$ $ = 2\sin x(1 + 2\cos x).$ $y’ = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {\sin x = 0}\\ {\cos x = – \frac{1}{2}} \end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = k\pi }\\ {x = \pm \frac{{2\pi }}{3} + k2\pi } \end{array}} \right.$ ($k \in Z$). $y” = 2\cos x + 4\cos 2x.$ Ta có: $y”(k\pi ) = \left\{ {\begin{array}{*{20}{l}} {2\:{\rm{nếu}}\:k\:{\rm{lẻ}}}\\ {6\:{\rm{nếu}}\:k\:{\rm{chẵn}}} \end{array}} \right.$ $ \Rightarrow y”(k\pi ) > 0$ (có thể viết: ${y”(k\pi ) = 4 + 2\cos k\pi }$). Nên hàm số đạt cực tiểu tại các điểm $x = k\pi $, ${y_{CT}} = y(kx)$ $ = \left\{ {\begin{array}{*{20}{l}} {0\:{\rm{nếu}}\:k\:{\rm{chẵn}}}\\ {4\:{\rm{nếu}}\:k\:{\rm{lẻ}}} \end{array}} \right..$ $y”\left( { \pm \frac{{2\pi }}{3} + k2\pi } \right) = – 3 < 0$ nên hàm số đạt cực đại tại các điểm: $x = \pm \frac{{2\pi }}{3} + k2\pi $, $k \in Z$, ${y_{CĐ}} = y\left( { \pm \frac{{2\pi }}{3} + k2\pi } \right) = \frac{9}{2}.$
Bài 13. Tìm các hệ số $a$, $b$, $c$, $d$ của hàm số $f(x) = a{x^3} + b{x^2} + cx + d$ sao cho hàm số $f$ đạt cực tiểu tại điểm $x = 0$, $f(0) = 0$ và đạt cực đại tại điểm $x = 1$, $f(1) = 1.$
Ta có $f'(x) = 3a{x^2} + 2bx + c$ $ \Rightarrow f'(0) = c$, $f'(1) = 3a + 2b + c.$ Vì $f(0) = 0$ $ \Rightarrow d = 0.$ Hàm số đạt cực tiểu tại $x = 0$ nên $f'(0) = 0$ $ \Rightarrow c = 0$, $f(1) = 1$ $ \Rightarrow a + b = 1.$ Hàm số đạt cực đại tại điểm $x = 1$ nên $f'(1) = 0$ $ \Rightarrow 3a + 2b = 0.$ Giải hệ: $\left\{ {\begin{array}{*{20}{l}} {a + b = 1}\\ {3a + 2b = 0} \end{array}} \right.$ ta được $a = – 2$, $b = 3.$ Vậy $f(x) = – 2{x^3} + 3{x^2}.$ Thử lại $f'(x) = – 6{x^2} + 6x$, $f”(x) = – 12x + 6.$ $f”(0) = 6 > 0.$ Hàm số đạt cực tiểu tại điểm $x = 0.$ $f”(1) = – 6 < 0.$ Hàm số đạt cực đại tại $x = 1.$ Đáp số: $a = -2$, $b = 3$, $c = 0$, $d = 0.$
Bài 14. Xác định các hệ số $a$, $b$, $c$ sao cho hàm số $f(x) = {x^3} + a{x^2} + bx + c$ đạt cực trị bằng $0$ tại $x = -2$ và đồ thị của hàm số đi qua $A(1;0).$
Cách 1. $f'(x) = 3{x^2} + 2ax + b.$ Điều kiện cần: Hàm số đạt cực trị bằng $0$ tại $x = – 2$ $ \Rightarrow f'( – 2) = 0$ $f( – 2) = 0.$ Hay $ – 4a + b + 12 = 0$ $(1)$ và $4a – 2b + c – 8 = 0$ $(2).$ Đồ thị đi qua $A(1;0)$ $ \Rightarrow a + b + c + 1 = 0.$ Giải hệ gồm ba phương trình $(1)$, $(2)$, $(3)$ ta được $a = 3$, $b = 0$, $c = -4.$ Điều kiện đủ: Xét $f(x) = {x^3} + 3{x^2} – 4.$ Ta có: đồ thị hàm số $f(x)$ đi qua $A(1;0).$ $f'(x) = 3{x^2} + 6x$ $ \Rightarrow f”(x) = 6x + 6.$ $f'( – 2) = 0$, $f”( – 2) = – 6 < 0$ nên $x = – 2$ là điểm cực đại và $f( – 2) = 0.$ Đáp số: $a = 3$, $b = 0$, $c = -4.$ Cách 2. Hướng dẫn: Yêu cầu bài toán tương đương với: $f( – 2) = 0$, $f'( – 2) = 0$, $f(1) = 0$, phương trình $f'(x) = 0$ có hai nghiệm phân biệt trong đó có một nghiệm $x = -2.$
Bài 15. Chứng minh rằng với mọi giá trị của $m$, hàm số $y = \frac{{{x^2} – m(m + 1)x + {m^3} + 1}}{{x – m}}$ luôn có cực đại và cực tiểu.
Hàm số được viết lại là: $y = x – {m^2} + \frac{1}{{x – m}}$, hàm số xác định với mọi $x \ne m.$ $y’ = 1 – \frac{1}{{{{(x – m)}^2}}}$ với $x \ne m$, $y’ = 0$ $ \Leftrightarrow {(x – m)^2} = 1$ $ \Leftrightarrow x = m – 1$ hoặc $x = m + 1.$ Bảng biến thiên:

Vậy với mọi giá trị của $m$, hàm số đạt cực đại tại $x = m -1$ và đạt cực tiểu tại $x = m + 1.$
Từ khóa » Cực Trị Của Hàm Số 12 Nâng Cao
-
Giải Toán 12 Nâng Cao Bài 2: Cực Trị Của Hàm Số
-
Các Dạng Toán Cơ Bản Và Nâng Cao Cực Trị Của Hàm Số
-
GIẢI TÍCH - TOÁN 12 NÂNG CAO
-
Cực Trị Của Hàm Số Lớp 12: Lý Thuyết, Cách Tìm Và Bài Tập
-
Giải Toán 12 Nâng Cao: Bài 2. Cực Trị Của Hàm Số - Toploigiai
-
[SGK Scan] ✓ Cực Trị Của Hàm Số - Sách Giáo Khoa
-
Tìm Cực Trị Của Các Hàm Số Sau. Bài 12 Trang 17 SGK Đại Số Và Giải ...
-
2 Dạng Bài Nâng Cao Về Cực Trị Của Hàm Số - Học Thật Giỏi
-
Bài 11, 12, 13 Trang 16, 17 Giải Tích 12 Nâng Cao: Cực Trị Của Hàm Số
-
Bài Toán Nâng Cao Cực Trị Hàm Số - Toán 12 - Thầy Trần Xuân Trường
-
Giáo án Giải Tích 12 Nâng Cao Tiết 4, 5: Cực Trị Của Hàm Số - Tài Liệu Text
-
Tìm Cực Trị Của Hàm Số Sau: Y = X Căn (4 - Haylamdo
-
Cực Trị Của Hàm Số – Giải Bài Tập SGK Toán 12
-
Giải Bài 11, 12, 13 Trang 16, 17 SGK Giải Tích 12 Nâng Cao