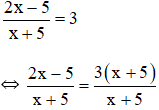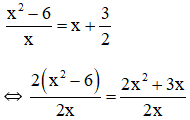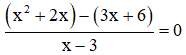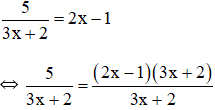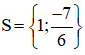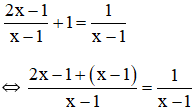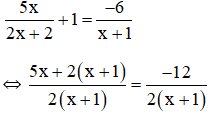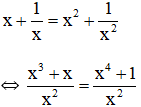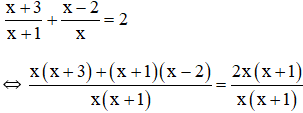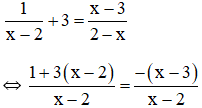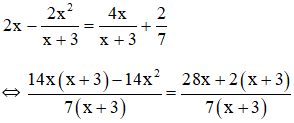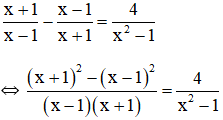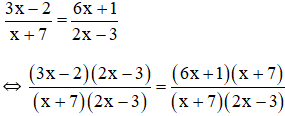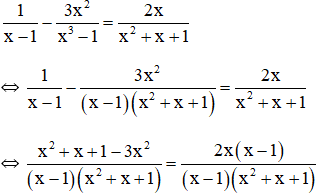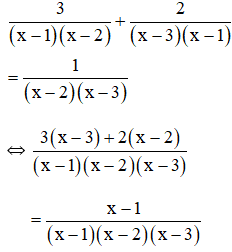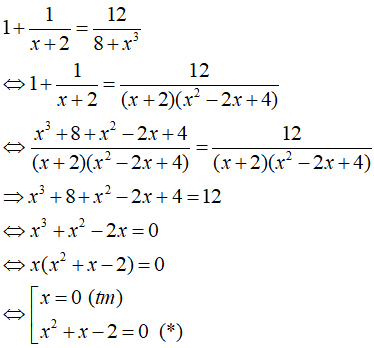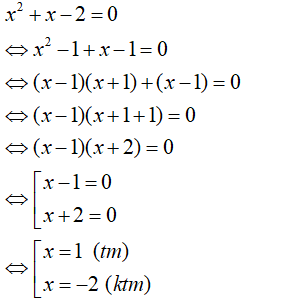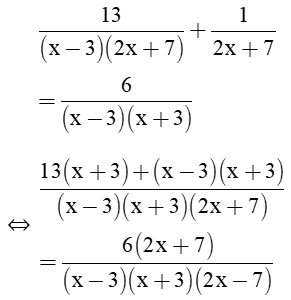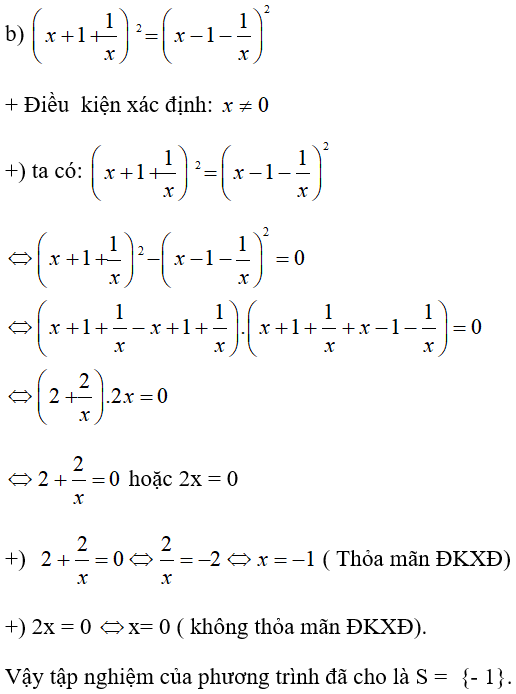Giải Toán Lớp 8 SGK Tập 2 Trang 20, 21, 22, 23 đầy đủ Nhất

Nội dung bài viết

1. Trả lời câu hỏi Toán lớp 8 SGK Tập 2 trang 19: 
2. Trả lời câu hỏi SGK Toán lớp 8 Tập 2 trang 20
3. Trả lời câu hỏi Sách giáo khoa Toán 8 Tập 2 trang 22
4. Giải bài 27 trang 22 SGK Toán tập 2 lớp 8
5. Giải bài 28 SGK Toán lớp 8 trang22 tập 2
6. Giải bài 29 trang 22, 23 tập 2 SGK Toán lớp 8
7. Giải bài 30 SGK Toán lớp 8 tập 2 trang 23
8. Giải bài 31 trang 23 SGK Toán lớp 8 tập 2
9. Giải bài 32 SGK Toán trang 23 lớp 8 tập 2 
10. Giải bài 33 lớp 8 SGK Toán tập 2 trang 23

Hướng dẫn giải sách giáo khoa Toán lớp 8 trang 20, 21, 22, 23 tập 2 bài: Phương trình chứa ẩn ở mẫu đầy đủ, chi tiết nhất. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài học sắp tới được tốt nhất.

Trả lời câu hỏi Toán lớp 8 SGK Tập 2 trang 19: 

Giá trị x = 1 có phải là nghiệm của phương trình hay không? Vì sao?

Lời giải

Giá trị x = 1 không phải là nghiệm của phương trình.

Vì tại x = 1 thì  có mẫu bằng 0, vô lí

Trả lời câu hỏi SGK Toán lớp 8 Tập 2 trang 20

Tìm điều kiện xác định của mỗi phương trình sau:

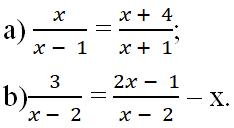
Lời giải

a) x – 1 ≠0 khi x ≠1 và x + 2 ≠0 khi x ≠- 2

Vậy ĐKXĐ của phương trình 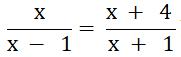 là x ≠1 và x ≠- 2

b) x – 2 ≠0 khi x ≠2

Vậy ĐKXĐ của phương trình 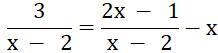 là x ≠2

Trả lời câu hỏi Sách giáo khoa Toán 8 Tập 2 trang 22

Giải các phương trình trong câu hỏi 2

Lời giải

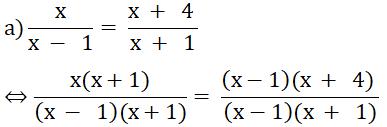
Suy ra x(x + 1) = (x - 1)(x + 4)

Ta có:

x(x + 1) = (x - 1)(x + 4)

⇔ x2 + x = x2 + 4x - x - 4

⇔ x = 3x - 4

⇔ 2x = 4

⇔ x = 2 (thỏa mãn ĐKXĐ)

Vậy tập nghiệm của phương trình là: S = {2}

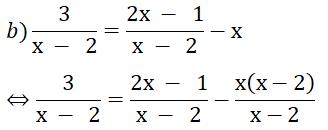
Suy ra 3 = 2x - 1 - x(x - 2)

⇔ 3 = 2x - 1-(x2 - 2x)

⇔ 3 = 2x - 1 - x2 + 2x

⇔ 3 = - 1 - x2

⇔ x2 = -4 (vô nghiệm)

Vậy tập nghiệm của phương trình là: S = ∅

Giải bài 27 trang 22 SGK Toán tập 2 lớp 8

Giải các phương trình:

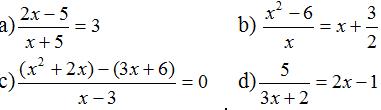
Lời giải:

a) Điều kiện xác định: x ≠ -5.

Suy ra: 2x – 5 = 3(x + 5)

⇔ 2x – 5 = 3x + 15

⇔ -5 – 15 = 3x – 2x

⇔ x = -20 (thỏa mãn điều kiện xác định).

Vậy phương trình có tập nghiệm S = {-20}.

b) Điều kiện xác định: x ≠ 0.

Suy ra: 2(x2 – 6) = 2x2 + 3x

⇔ 2x2 – 12 – 2x2 – 3x = 0

⇔ - 12 - 3x = 0

⇔ -3x = 12

⇔ x = -4 (thỏa mãn điều kiện xác định)

Vậy phương trình có tập nghiệm S = {-4}.

c) Điều kiện xác định: x ≠ 3.

Suy ra: (x2 + 2x) – (3x + 6) = 0

⇔ x(x + 2) – 3(x + 2) = 0

⇔ (x – 3)(x + 2) = 0

⇔ x – 3 = 0 hoặc x + 2 = 0

+ x – 3 = 0 ⇔ x = 3 (Không thỏa mãn đkxđ)

+ x + 2 = 0 ⇔ x = -2 (Thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = {-2}.

d) Điều kiện xác định: x ≠ -2/3.

Suy ra: 5 = (2x – 1)(3x + 2) hay (2x – 1)(3x + 2) = 5

⇔ 2x.3x + 2x.2 – 1.3x – 1.2 = 5

⇔ 6x2 + 4x – 3x – 2 – 5 = 0

⇔ 6x2 + x – 7 = 0.

⇔ 6x2 – 6x + 7x – 7 = 0

(Tách để phân tích vế trái thành nhân tử)

⇔ 6x(x – 1) + 7(x – 1) = 0

⇔ (6x + 7)(x – 1) = 0

⇔ 6x + 7 = 0 hoặc x – 1 = 0

+ 6x + 7 = 0 ⇔ 6x = - 7 ⇔ x = -7/6 (thỏa mãn đkxđ)

+ x – 1 = 0 ⇔ x = 1 (thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm 

Giải bài 28 SGK Toán lớp 8 trang22 tập 2

Giải các phương trình:

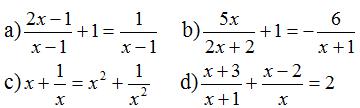
Lời giải:

a) Điều kiện xác định: x ≠ 1.

Suy ra: 2x – 1 + x – 1 = 1

⇔ 3x – 2 = 1

⇔ 3x = 3

⇔ x = 1 (không thỏa mãn điều kiện xác định).

Vậy phương trình vô nghiệm.

b) Điều kiện xác định: x ≠ -1.

Suy ra: 5x + 2( x+ 1) = - 12

⇔ 5x + 2x + 2 = -12

⇔ 7x + 2 = -12

⇔ 7x = -14

⇔ x = -2 (thỏa mãn đkxđ)

Vậy phương trình có tập nghiệm S = {-2}

c) Điều kiện xác định: x ≠ 0.

Suy ra: x3 + x = x4 + 1

⇔ x4 + 1 – x – x3 = 0

⇔ (x4 – x3) + (1 – x) = 0

⇔ x3(x – 1) – (x – 1) = 0

⇔ (x3 – 1)(x – 1) = 0

⇔ (x – 1)(x2 + x + 1)(x – 1) = 0

⇔ (x – 1)2. (x2 + x + 1) = 0

⇔ x – 1 = 0

(vì 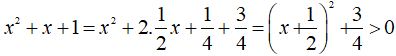 với mọi x).

⇔ x = 1 (thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = {1}.

d) Điều kiện xác định: x ≠ 0 và x ≠ -1.

Suy ra: x(x + 3) + (x + 1)(x – 2) = 2.x(x + 1)

⇔ x(x + 3) + (x + 1)(x – 2) – 2x(x + 1) = 0

⇔ x2 + 3x + x2 – 2x + x – 2 – (2x2 + 2x) = 0

⇔ x2 + 3x + x2 – 2x + x – 2 – 2x2 - 2x = 0

⇔ x2 + x2 – 2x2 + 3x + x – 2x – 2x – 2 = 0

⇔ 0x – 2 = 0

⇔ 0x = 2

Phương trình vô nghiệm.

Giải bài 29 trang 22, 23 tập 2 SGK Toán lớp 8

Bạn Sơn giải phương trình

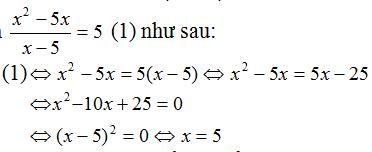
Bạn Hà cho rằng Sơn giải sai vì đã nhân hai vế với biểu thức x – 5 có chứa ẩn. Hà giải bằng cách rút gọn vế trái như sau:

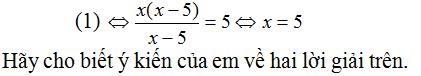
Lời giải:

Giải bài 30 SGK Toán lớp 8 tập 2 trang 23

Giải các phương trình:

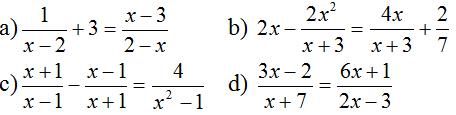
Lời giải:

a) Điều kiện xác định: x ≠ 2.

Suy ra: 1 + 3(x – 2) = -(x – 3)

⇔ 1 + 3x – 6 = -x + 3

⇔ 3x + x = 3 + 6 – 1

⇔ 4x = 8

⇔ x = 2 (không thỏa mãn đkxđ).

Vậy phương trình vô nghiệm.

b) Điều kiện xác định: x ≠ -3.

Suy ra: 14x(x + 3) – 14x2 = 28x + 2(x + 3)

⇔ 14x2 + 42x – 14x2 = 28x + 2x + 6

⇔ 42x – 28x – 2x = 6

⇔ 12x = 6

⇔ x = 1/2. (thỏa mãn điều kiện)

Vậy phương trình có tập nghiệm S = {1/2}.

c) Điều kiện xác định: x ≠ ±1.

Suy ra: x2 + 2x + 1 – (x2 – 2x + 1) = 4

⇔ x2 + 2x + 1 – x2 + 2x – 1 = 4

⇔ 4x = 4

⇔ x = 1 (không thỏa mãn đkxđ)

Vậy phương trình vô nghiệm.

d) Điều kiện xác định: x ≠ -7; x ≠ 3/2.

Suy ra: (3x – 2)(2x – 3) = (6x + 1)(x + 7)

⇔ 6x2 – 9x – 4x + 6 = 6x2 + 42x + x + 7

⇔ - 4x - 9x - 42x - x = 7 - 6

⇔ - 56x = 1

⇔ x = -1/56 (thỏa mãn đkxđ)

Vậy phương trình có tập nghiệm S = {-1/56}.

Giải bài 31 trang 23 SGK Toán lớp 8 tập 2

Giải các phương trình:

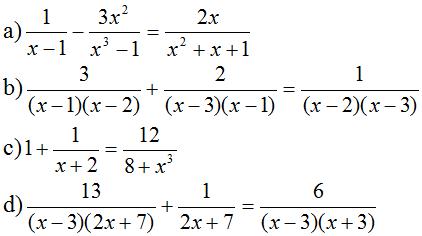
Lời giải:

a) + Tìm điều kiện xác định :

x2 + x + 1 = (x2 + x + ¼) + ¾ = (x + ½)2 + ¾ > 0 với mọi x ∈ R.

Do đó x2 + x + 1 ≠ 0 với mọi x ∈ R.

x3 – 1 ≠ 0 ⇔ (x – 1)(x2 + x + 1) ≠ 0 ⇔ x – 1 ≠ 0 ⇔ x ≠ 1.

Vậy điều kiện xác định của phương trình là x ≠ 1.

+ Giải phương trình:

⇒ x2 + x + 1 – 3x2 = 2x(x – 1)

⇔ -2x2 + x + 1 = 2x2 – 2x

⇔ - 4x2 + 3x + 1 = 0

⇔ - 4x2 + 4x - x + 1 = 0

⇔ - 4x(x – 1) – ( x – 1) = 0

⇔ (- 4x - 1)(x – 1) = 0

⇔ - 4x - 1 = 0 hoặc x – 1 = 0

+) Nếu - 4x - 1 = 0 ⇔ - 4x = 1 ⇔ x = -1/4 (thỏa mãn đkxđ)

+) Nếu x – 1 = 0 ⇔ x = 1 (không thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = {-1/4}.

b) Điều kiện xác định: x ≠ 1; x ≠ 2; x ≠ 3.

⇒ 3(x – 3) + 2(x – 2) = x – 1

⇔ 3x – 9 + 2x – 4 = x – 1

⇔ 3x + 2x – x = 9 + 4 – 1

⇔ 4x = 12

⇔ x = 3 (không thỏa mãn điều kiện xác định)

Vậy phương trình vô nghiệm.

c)

+) Ta có; 8+x3 = (2 + x).( 4 - 2x+ x2 )

Mà 4 - 2x + x2 = (1 – 2x + x2 ) + 3 = ( 1- x)2 + 3 >0 với mọi x.

Do đó: 8 + x3 ≠ 0 ⇔ 2 + x ≠ 0 ⇔ x ≠ -2

+) Điều kiện xác định: x ≠ -2.

Giải phương trình (*):

Vậy tập nghiệm của phương trình là S = {0; 1}.

d) Điều kiện xác định: x ≠ ±3; x ≠ -7/2.

⇒ 13(x + 3) + (x – 3)(x + 3) = 6(2x + 7)

⇔ 13x + 39 + x2 – 9 = 12x + 42

⇔ x2 + x – 12 = 0

⇔ x2 +4x – 3x – 12 = 0

⇔ x(x + 4) – 3(x + 4) = 0

⇔ (x – 3)(x + 4) = 0

⇔ x – 3 = 0 hoặc x + 4 = 0

x – 3 = 0 ⇔ x = 3 (không thỏa mãn đkxđ)

x + 4 = 0 ⇔ x = -4 (thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = {-4}.

Giải bài 32 SGK Toán trang 23 lớp 8 tập 2 

Giải các phương trình:

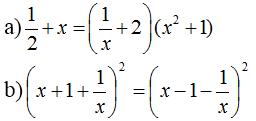
Lời giải:

Giải bài 33 lớp 8 SGK Toán tập 2 trang 23

Tìm các giá trị của a sao cho mỗi biểu thức sau có giá trị bằng 2:

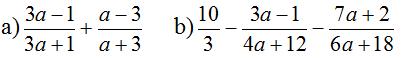
Lời giải:

Biểu thức có giá trị bằng 2 thì:

CLICK NGAY vào nút TẢI VỀ dưới đây để giải toán lớp 8 SGK tập 2 trang 20, 21, 22, 23 tập 2 file word, pdf hoàn toàn miễn phí.