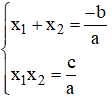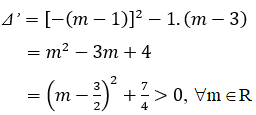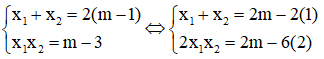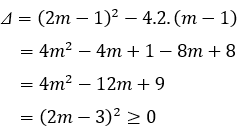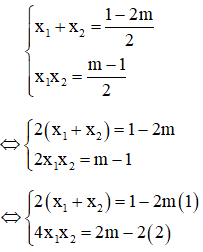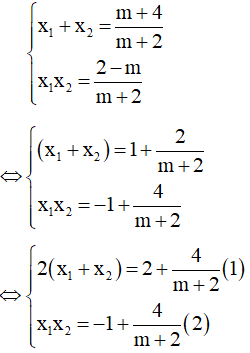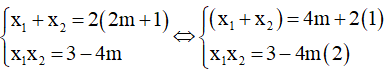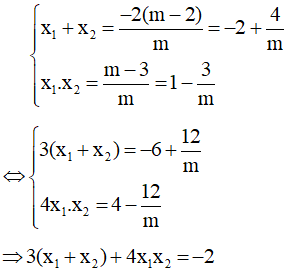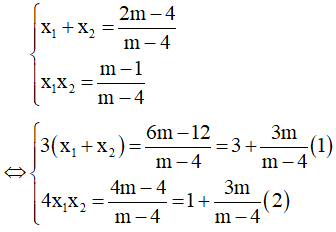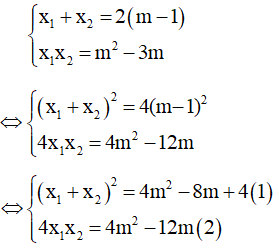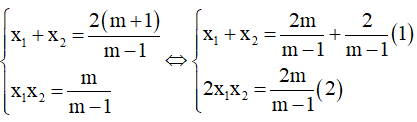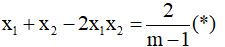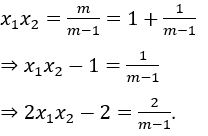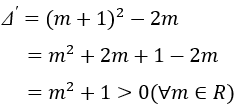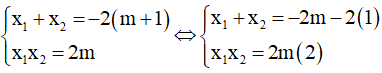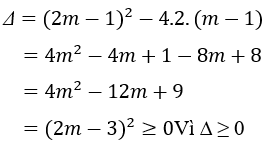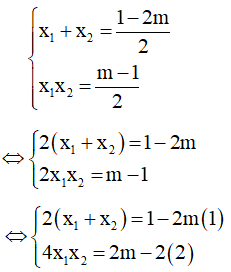Tìm Hệ Thức Liên Hệ Giữa X1 X2 độc Lập Với M

Tìm hệ thức liên hệ giữa hai nghiệm không phụ thuộc vào tham số | Tìm hệ thức liên hệ giữa x1 x2 độc lập với m

A. Phương pháp giải

Để tìm hệ thức giữa các nghiệm x1, x2của phương trình bậc hai không phụ thuộc tham số ta làm như sau:

B1: Tìm điều kiện để phương trình có 2 nghiệm x1, x2(∆ ≥ 0)

B2: áp dụng Vi-et tìm:

B3: Biến đổi kết quả không chứa tham số nữa

Ví dụ 1: Cho phương trình x2-2(m-1)x+m-3=0 (m là tham số). Tìm một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho mà không phụ thuộc vào m.

Giải

Vậy phương trình đã cho luôn có hai nghiệm phân biệt x1, x2

Theo hệ thức Vi-ét, ta có:

Lấy (1) – (2): x1+ x2- 2 x1x2= 4 không phụ thuộc vào m.

Ví dụ 2: Cho phương trình 2x2+ (2m – 1)x + m – 1 = 0 (m là tham số). Tìm một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho mà không phụ thuộc vào m.

Giải

Vì ∆ ≥ 0 với mọi m nên phương trình luôn có hai nghiệm x1, x2

Theo hệ thức Vi-et ta có:

Lấy (1) + (2): 2(x1+ x2) +4x1x2= -1 không phụ thuộc vào m

B. Bài tập

Câu 1:Cho phương trình (m + 2)x2- (m + 4)x + 2 - m = 0 (m là tham số). Khi phương trình có nghiệm, tìm một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho không phụ thuộc vào m.

A. 3(x1+ x2) - x1x2= 4

B. (x1+ x2) + 2x1x2= 0

C. 2(x1+ x2) - x1x2= 3

D. (x1+ x2) + x1x2= 2

Giải

Giả sử phương trình có hai nghiệm x1, x2

Theo hệ thức Vi-et ta có:

Lấy (1) - (2): 2(x1+ x2) - x1x2= 3 không phụ thuộc vào m

Đáp án đúng là C

Câu 2:Cho phương trình x2- 2(2m + 1)x + 3 – 4m = 0 (m là tham số). Khi phương trình có nghiệm, tìm một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho không phụ thuộc vào m.

A. x1+ x2- x1x2= 4

B. x1+ x2+ x1x2= 5

C. x1+ x2- x1x2= 3

D. x1+ x2+ x1x2= 2

Giải

Giả sử phương trình có hai nghiệm x1, x2

Theo hệ thức Vi-et ta có:

Lấy (1) + (2): x1+ x2+ x1x2= 5 không phụ thuộc vào m

Đáp án đúng là B

Câu 3:Cho phương trình mx2+ 2(m – 2)x + m – 3 = 0 (m là tham số). Khi phương trình có nghiệm, tìm một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho không phụ thuộc vào m.

A. 2(x1+ x2) - x1x2= 3

B. x1+ x2- 4x1x2= 2

C. x1+ x2- 3x1x2= 1

D. 3(x1+ x2) + 4x1x2= -2

Giải

Giả sử phương trình có hai nghiệm x1, x2

Khi đó theo Vi-ét ta có:

Đây là hệ thức liên hệ giữa các nghiệm không phụ thuộc vào m.

Đáp án đúng là D

Câu 4:Cho phương trình (m – 4)x2- 2(m – 2)x + m – 1 = 0 (m là tham số). Khi phương trình có nghiệm, tìm một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho không phụ thuộc vào m.

A. 3(x1+ x2) - 4x1x2= 2

C. x1+ x2- x1x2= 2

B. x1+ x2- 4x1x2= 0

D. 3(x1+ x2) + 4x1x2= -2

Giải

Giả sử phương trình có hai nghiệm x1, x2

Theo hệ thức Vi-et ta có:

Lấy (1) - (2): 3(x1+ x2) - 4x1x2= 2 không phụ thuộc vào m

Đáp án là A

Câu 5:Cho phương trình x2- 2(m – 1)x + m2– 3m = 0 (m là tham số). Khi phương trình có nghiệm, tìm một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho mà không phụ thuộc vào m.

A. (x1+ x2)2- x1x2- (x1+ x2) = 5

B. (x1+ x2)2- 2x1x2- 4(x1+ x2) = 8

C. (x1+ x2)2- 4x1x2- 2(x1+ x2) = 6

D. (x1+ x2)2- 4x1x2- 2(x1+ x2) = 8

Giải

Giả sử phương trình có hai nghiệm x1, x2

Theo hệ thức Vi-et ta có:

Lấy (1) - (2): (x1+ x2)2- 4x1x2= 4m + 4(*)

Mặt khác từ: x1+ x2= 2m - 2 ⇒ 2(x1+ x2) = 4m - 4 ⇒ 2(x1+ x2) + 4 = 4m. Thay vào (*) ta được:

(x1+ x2)2- 4x1x2= 2(x1+ x2) + 4 + 4

⇔ (x1+ x2)2- 4x1x2- 2(x1+ x2) = 8 không phụ thuộc vào m

Đáp án đúng là D

Câu 6:Cho phương trình (m – 1)x2- 2(m + 1)x + m = 0 (m là tham số). Khi phương trình có nghiệm, tìm một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho không phụ thuộc vào m.

A. x1+ x2- x1x2= 2

B. x1+ x2- 4x1x2= -2

C. x1+ x2- 3x1x2= -1

D. x1+ x2+ 5x1x2= 7

Giải

Giả sử phương trình có hai nghiệm x1, x2

Theo hệ thức Vi-et ta có:

Lấy (1) - (2):

Mặt khác từ:

Thay vào (*) ta được: x1+ x2- 2x1x2= 2x1x2- 2 không phụ thuộc vào m

Đáp án đúng là B

Câu 7:Cho phương trình x2+ 2(m + 1)x + 2m = 0 (m là tham số). Tìm một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho mà không phụ thuộc vào m.

A. (x1+ x2) + x1x2= -2

B. 2(x1+ x2) + x1x2= 0

C. (x1+ x2) + 2x1x2= -1

D. (x1+ x2) - x1x2= -2

Giải

Vì ∆ꞌ > 0 với mọi m nên phương trình luôn có hai nghiệm x1, x2

Theo hệ thức Vi-et ta có :

Lấy (1) + (2): (x1+ x2) + x1x2= -2 không phụ thuộc vào m

Đáp án đúng là A

Câu 8:Cho phương trình 2x2+ (2m – 1)x + m – 1 = 0 (m là tham số). Tìm một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho mà không phụ thuộc vào m.

A. (x1+ x2) - 4x1x2= -4

B. 2(x1+ x2) + 4x1x2= 0

C. 2(x1+ x2) + 4x1x2= -1

D. (x1+ x2) - x1x2= 2

Giải

Vì ∆ ≥ 0 với mọi m nên phương trình luôn có hai nghiệm x1, x2

Theo hệ thức Vi-et ta có :

Lấy (1) + (2): 2(x1+ x2) +4x1x2= -1 không phụ thuộc vào m

Đáp án đúng là C