Cách Tìm Ước Chung Lớn Nhất (ƯCLN), Bội Chung Nhỏ Nhất (BCNN ...
Có thể bạn quan tâm
Vậy Ước chung lớn nhất và Bội chung nhỏ nhất là gì? Cách tìm Ước chung lớn nhất (ƯCLN) và Bội chung nhỏ nhất (BCNN) như thế nào? Chúng ta cùng tìm hiểu qua bài viết dưới đây. Sau đó vận dụng vào giải một số bài tập minh họa để rèn kỹ năng giải toán.
» xem thêm: Các dạng toán về phân số cực hay
I. Kiến thức Ước và Bội cần nhớ
1. Định nghĩa ước và bội
- Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b là ước của a.
* Ví dụ: Số 8 có là bội của 4 vì 8 chia hết cho 4. Nhưng số 8 không là bội của 3 vì 8 không chia hết cho 3.
2. Cách tìm ước và bội
* Kí hiệu: B(a): tập hợp các bội của a. Ư(a): tập hợp các ước của a.
• Cách tìm bội của 1 số: Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lượt cho 1, 2, 3,..
* Ví dụ: Tìm bội của số 5 như sau:
B(5) = {5.1; 5.2; 5.3; 5.4; ...} = {5; 10; 15; 20;...}
• Cách tìm ước của 1 số: Ta có thể tìm các ước của một số a (a > 1) bằng cách lần lượt chia số a cho số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.
* Ví dụ: Tìm các ước của 8, 10, 12, 13 như sau:
Ư(8) = {8; 4; 2; 1}
Ư(10) = {10; 5; 1}
Ư(12) = {12; 6; 4; 2; 1}
Ư(13) = {12; 1}.
3. Một số bài tập tìm ước và bội
* Bài 111 trang 44 sgk Toán 6 Tập 1:
a) Tìm các bội của 4 trong các số 8; 14; 20; 25.
b) Viết tập hợp các bội của 4 nhỏ hơn 30.
c) Viết dạng tổng quát các số là bội của 4.
° Lời giải:
a) Trong các số 8; 14; 20; 25 chỉ có 8 và 20 chia hết cho 4.
→ Vậy bội của 4 là 8; 20.
b) Các số chia hết cho 4 mà nhỏ hơn 30 là 0; 4; 8; 12; 16; 20; 24; 28.
→ Vậy tập hợp bội của 4 nhỏ hơn 30 là B = {0; 4; 8; 12; 16; 20; 24; 28}.
c) Các số tự nhiên chia hết cho 4 đều có dạng 4.k (với k ∈ N).
→ Vậy dạng tổng quát các số là bội của 4 là 4k (với k ∈ N).
* Bài 112 trang 44 sgk Toán 6 Tập 1: Tìm các ước của 4, của 6, của 9, của 13 và của 1.
° Lời giải:
a) Lần lượt chia 4 cho 1 ,2 ,3 ,4 ta thấy 4 chia hết cho 1, 2, 4
→ Vậy Ư(4) = {1, 2, 4}
b) Lần lượt chia 6 cho 1, 2, 3, 4, 5, 6 ta thấy 6 chia hết 1, 2, 3, 6.
→ Vậy Ư(6) = {1, 2, 3, 6}.
c) Lần lượt chia 9 cho 1, 2, 3, 4, 5, 6, 7, 8, 9 ta thấy 9 chia hết cho 1, 3, 9
→ Vậy Ư(9) = {1; 3; 9}.
d) Lần lượt chia 13 cho 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13. Ta thấy 13 chia hết cho 1 và 13.
→ Vậy Ư(13) = {1; 13}
e) Ư(1) = {1}.
II. Khái niệm ước chung, ước chung lớn nhất (ƯCLN) và cách tìm
1. Ước chung là gì?
• Ước chung của 2 hay nhiều số là ước của tất cả các số đó.
* Ví dụ: Ư(4) = {1; 2; 4} và Ư(6) = {1; 2; 3; 6}
Ước chung của 4 và 6 ký hiệu là: ƯC(4,6) = {1;2}.
⇒ x ∈ ƯC(a,b) nếu a 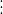 x và b
x và b 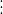 x;
x;
2. Ước chung lớn nhất (ƯCLN)
• Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp ước chung.
* Ví dụ: Ư(12) = {1; 2; 3; 4; 6; 12} và Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}
→ ƯC(12,30) = {1; 2; 3; 6} số lớn nhất trong tập hợp ước chung là 6.
→ Ta nói 6 là ước chung lớn nhất (ƯCLN) của 12 và 30, ký hiệu ƯCLN(12,30)=6.
3. Cách tìm ước chung lớn nhất (ƯCLN)
• Muốn tìm ước chung lớn nhất của hai hay nhiều số lớn hơn 1, ta thực hiện các bước sau:
- Bước 1: Phẫn tích mỗi số ra thừa số nguyên tố
- Bước 2: Chọn ra các thừa số nguyên tố chung
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN cần tìm.
III. Khái niệm bội chung, bội chung nhỏ nhất (BCNN) và cách tìm
1. Bội chung là gì?
• Bội chung của hai hay nhiều số là bội của tất cả các số đó
* Ví dụ: B(4) = {0; 4; 8; 12; 16, 20; 24;...} và B(6) = {0; 6; 12; 18; 24;...}
Ký hiệu bội chung của 4 và 6 là BC(4,6) = {0; 12; 24;...}
⇒ x ∈ BC(a,b) nếu x 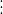 a và x
a và x 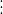 b;
b;
2. Bội chung nhỏ nhất (BCNN)
• Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.
* Ví dụ: B(4) = {0; 4; 8; 12; 16, 20; 24;...} và B(6) = {0; 6; 12; 18; 24;...}
→ BC(4,6) = {0; 12; 24;...} Số nhỏ nhất khác 0 trong tập hợp bội chung là 12;
→ 12 là bội chung nhỏ nhất (BCNN) của 4 và 6, ký hiệu; BCNN(4,6)=12.
3. Cách tìm bội chung nhỏ nhất (BCNN)
• Muốn tìm bội chung nhỏ nhất (BCNN) của hai hay nhiều số lớn hơn 1, ta thực hiện các bước sau:
- Bước 1: Phân tích mỗi số ra thừa số nguyên tố
- Bước 2: Chọn ra các thừa số nguyên tố chung và riêng
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN cần tìm.
IV. Một số bài tập vận dụng tìm ước chung lớn nhất, bội chung nhỏ nhất
* Bài 139 trang 56 SGK Toán 6 Tập 1: Tìm ƯCLN của:
a) 56 và 140 ; b) 24, 84, 180
c) 60 và 180 ; d) 15 và 19
° Lời giải:
a) – Phân tích ra thừa số nguyên tố: 56 = 23.7; 140 = 22.5.7
– Các thừa số nguyên tố chung là 2; 7.
⇒ ƯCLN(56, 140) = 22.7 = 28 (số mũ của 2 nhỏ nhất là 2; số mũ của 7 đều bằng 1).
b) Ta có: 84 = 22 .3 .7; 24 = 23.3; 180 = 22.32.5
⇒ ƯCLN(24, 84, 180) = 22.3 = 12.
c)- Cách 1: 60 = 22.3.5; 180 = 22.32.5
⇒ƯCLN (60, 180) = 22.3.5 = 60.
- Cách 2: 60 là ước của 180 nên ƯCLN (60; 180) = 60.
* Nhận xét: Cách 1 là cách thường dùng cho mọi bài toán tìm ƯCLN, cách 2 dùng cho 1 số trường hợp đặc biệt ƯCLN là 1 trong các số cần tìm ước.
d) Ta có: 15 = 3.5; 19 = 19
⇒ ƯCLN(15, 19) = 1.
* Bài 140 trang 56 SGK Toán 6 Tập 1: Tìm ƯCLN của:
a) 16, 80, 176 ; b) 18, 30, 77
° Lời giải:
a) Cách 1: 16 = 24 ; 80 = 24.5 ; 176 = 24.11
⇒ ƯCLN(16, 80, 176) = 24 = 16.- Cách 2: 80 ⋮ 16; 176 ⋮ 16 nên 16 là ước của 80; 176.
→ Do đó ƯCLN(16, 80, 176) = 16.
b) Ta có: 18 = 2.32 ; 30 = 2.3.5 ; 77=7.11
⇒ ƯCLN(18, 30, 77) = 1 (vì không có thừa số nguyên tố nào chung).
* Bài 142 trang 56 SGK Toán 6 Tập 1: Tìm ƯCLN rồi tìm các ước chung của:
a) 16 và 24 ; b) 180 và 234 ; c) 60, 90, 135
° Lời giải:
a) Ta có 16 = 24 và 24 = 23.3 ⇒ ƯCLN (16, 24) = 23 = 8.
→ ƯC(16, 24) = Ư(8) = {1; 2; 4; 8}.
b) Ta có 180 = 22.32.5 và 234 = 2.32.13 ⇒ ƯCLN(180, 234) = 2.32 = 18.
→ ƯC(180, 234) = Ư(18) = {1; 2; 3; 6; 9; 18}.
c) 60 = 22 .3.5; 90 = 2.32.5; 135 = 33 .5
⇒ ƯCLN(60, 90, 135) = 3.5 = 15.
→ ƯC(60, 90, 135) = Ư(15) = {1; 3; 5; 15}.
* Bài 143 trang 56 SGK Toán 6 Tập 1: Tìm số tự nhiên a lớn nhất, biết rằng 420 ⋮ a và 700 ⋮ a.
° Lời giải:
- Vì 420 ⋮ a và 700 ⋮ a nên a ∈ ƯC(420; 700).
- Theo bài ra, a là số tự nhiên lớn nhất nên a = ƯCLN(420; 700).
- Ta có: 420 = 22.3.5.7; 700 = 22.52.7
⇒ ƯCLN(420, 700) = 22.5.7 = 140
- Kết luận: Vậy a = 140.
* Bài 145 trang 56 SGK Toán 6 Tập 1: Lan có một tấm bìa hình chữ nhật kích thước 75cm và 105cm. Lan muốn cắt tấm bia thành các mảnh nhỏ hình vuông bằng nhau sao cho tấm bìa được cắt hết, không còn thừa mảnh nào. Tính độ dài lớn nhất của cạnh hình vuông (số đo cạnh của hình vuông nhỏ là một số tự nhiên với đơn vị xentimét).
° Lời giải:
- Để tấm bìa được cắt không còn thừa mảnh nào thì cạnh hình vuông phải là ước của chiều rộng và chiều dài tấm bìa.
- Chiều rộng bằng 75cm, chiều dài bằng 105cm.
- Do đó cạnh hình vuông phải là một trong các ƯC(75, 105).
- Độ dài lớn nhất của cạnh hình vuông là ƯCLN(75, 105).
- Ta có : 75 = 3.52 ; 105 = 3.5.7
⇒ ƯCLN(75, 105) = 3.5 = 15.
- Kết luận: Vậy cạnh hình vuông lớn nhất là 15cm.
* Bài 149 trang 59 SGK Toán 6 Tập 1: Tìm BCNN của:
a) 60 và 280 ; b) 84 và 108 ; c) 13 và 15
° Lời giải:
a) – Phân tích ra thừa số nguyên tố: 60 = 22.3.5; 280 = 23.5.7
– Chọn ra các thừa số nguyên tố chung và riêng: 2; 3; 5; 7.
– Lập tích: mỗi thừa số lấy với sỗ mũ lớn nhất: số mũ lớn nhất của 2 là 3; số mũ lớn nhất của 3; 5; 7 là 1.
→ BCNN(60, 280) = 23.3.5.7 = 840.
b) Ta có: 84 = 22.3.7; 108 = 22.33
⇒ BCNN(84, 108) = 22.33.7 = 756
c) Ta có: 13 = 13; 15 = 3.5
⇒ BCNN(13, 15) = 3.5.13 = 195.
* Bài 150 trang 59 SGK Toán 6 Tập 1: Tìm BCNN của:
a) 10, 12, 15 ; b) 8, 9, 11 ; c) 24, 40, 168
° Lời giải:
a) Ta có: 10 = 2.5; 12 = 22.3; 15 = 3.5
⇒ BCNN(10, 12, 15) = 22.3.5 = 60.
b) Ta có: 8 = 23 ; 9 = 32; 11 = 11⇒ BCNN(8, 9, 11) = 23.32.11 = 792.
c) Ta có: 24 = 23.3; 40 = 23.5; 168 = 23.3.7
⇒ BCNN(24, 40, 168) = 23.3.5.7 = 840.
* Bài 152 trang 59 SGK Toán 6 Tập 1: Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a chia hết cho 15 và a chia hết cho 18.
° Lời giải:
- Ta có: a ⋮ 15 và a ⋮ 18 ⇒ a ∈ BC(15, 18).
- Theo bài ra, a là số nhỏ nhất nên a = BCNN(15, 18).
- Mà 15 = 3.5; 18 = 2.32.
⇒ BCNN(15, 18) = 2.32.5 = 90.
- Kết luận: Vậy a = 90.
* Bài 154 trang 59 SGK Toán 6 Tập 1: Học sinh lớp 6C khi xếp hàng 2, hàng 3, hàng 4, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng từ 35 đến 60. Tính số học sinh lớp 6C.
° Lời giải:
+ Ta gọi số học sinh lớp 6C là a.
- Vì học sinh xếp hàng 2, hàng 3, hàng 4, hàng 8 đều vừa đủ nên a là bội của 2, 3, 4, 8. Hay a ∈ BC(2; 3; 4; 8).
+ Ta cần tìm BC(2, 3, 4, 8):
- Ta có: 2 = 2; 3 = 3; 4 = 22; 8 = 23
⇒ BCNN(2, 3, 4, 8) = 23.3 = 24.
⇒ BC(2, 3, 4, 8) = B(24) = {0; 24; 48; 72;...}
- Vì số học sinh trong khoảng từ 35 đến 60 nên suy ra a = 48.
- Kết luận: Số học sinh lớp 6C là 48.
Từ khóa » Tính Chất Của Ucln Và Bcnn
-
CHUYÊN ĐỀ UCLN VÀ BCNN
-
CHUYÊN ĐỀ ƯỚC - BỘI – UCLN – BCNN
-
Lý Thuyết ước Chung Lớn Nhất, Bội Chung Nhỏ Nhất Toán 6
-
Một Dạng Toán Về ƯCLN Và BCNN - Số Học 6
-
Ước Số Chung Lớn Nhất – Wikipedia Tiếng Việt
-
Bội Số Chung Nhỏ Nhất – Wikipedia Tiếng Việt
-
Các Tính Chất Ước Số Chung Lớn Nhất - Tieng Wiki
-
Chuyên đề Bội Chung Nhỏ Nhất Và Ước Chung Lớn Nhất - Tài Liệu Text
-
Ước Số Chung Lớn Nhất - VOER
-
Ước Chung Lớn Nhất Và Các Bước Tìm ƯCLN - Giáo Viên Việt Nam
-
Chuyên đề Bội – Ước – ƯCLN – BCNN - Bồi Dưỡng HSG Toán 6
-
Nêu Các Quy Tắc Tìm ƯCLN,BCNN Của Hai Hay Nhiều Số. Tìm Mối ...
-
[Sách Giải] Bài 17: Ước Chung Lớn Nhất. Bội Chung Nhỏ Nhất