Số Phức Nghịch Đảo Là Gì? Cách Tìm Bằng Máy Tính Cầm Tay

Warning: mysqli_query(): (HY000/1): Can't create/write to file '/tmp/#sql-temptable-b851-b8d88-10c4e.MAI' (Errcode: 28 "No space left on device") in /opt/bitnami/wordpress/wp-includes/wp-db.php on line 2162

Số phức nghịch đảo là kiến thức quan trọng của chương trình Toán học lớp 12. Vậy số phức là gì? Định nghĩa số phức nghịch đảo và cách tìm bằng máy tính cầm tay ra sao? Các em hãy cùng Team Marathon Education tìm hiểu về phần kiến thức này qua bài viết dưới đây.

>>> Xem thêm: Số Phức Đối Là Gì? Cách Tìm Điểm Biểu Diễn Của Số Phức Đối

>>> Xem thêm: Dạng Bài Tập Và Cách Giải Bất Phương Trình Toán Lớp 10

Số phức là gì?

Trong Tiếng Anh, số phức được gọi là Complex Number (Complex là phức hợp, Number là số). Nghĩa là số phức bao gồm nhiều thành phần để cấu tạo nên nó. Cụ thể, tập hợp số phức gồm các số có dạng a + bi. Trong đó, a và b là các số thực và i là đơn vị ảo thỏa i2 = -1. Các em có được:

\Complex = {\lbrace a+bi|a,b \in \R \rbrace}

Mô đun của số phức

\begin{aligned} &\footnotesize \text{Giả sử số phức z = a + bi được biểu diễn bởi điểm M (a;b) trên một mặt phẳng tọa} \\ &\footnotesize \text{độ Oxy. Khi đó, độ dài của vectơ }\overrightarrow{OM} \ \text{được gọi là mô đun của số phức z và được kí }\\ &\footnotesize \text{hiệu là |z|. Vậy }|z|=|\overrightarrow{OM}|=\sqrt{a^2+b^2} \end{aligned}

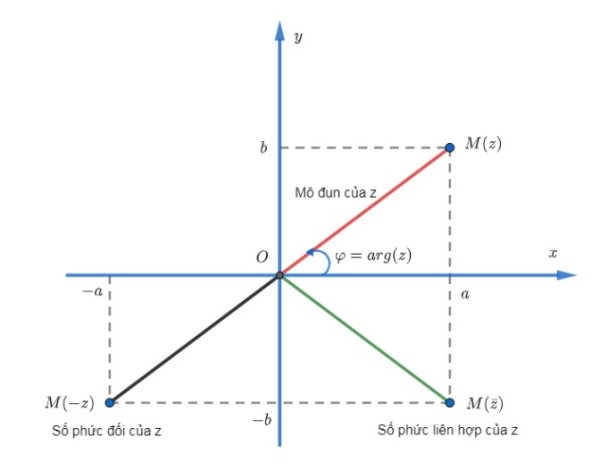
Số phức liên hợp

\begin{aligned} &\footnotesize \text{Cho số phức z = a+ bi. Các em gọi z = a - bi là số phức liên hợp của z và được kí }\\ &\footnotesize \text{hiệu là } \overline{z}=a-bi \end{aligned}

Chú ý:

• Tổng một số phức và số phức liên hợp của nó bằng 2 lần phần thực của số phức đó.
• Tích một số phức và số phức liên hợp của nó bằng bình phương mô đun số phức đó.

Cực Trị Của Hàm Số Lớp 12: Lý Thuyết, Cách Tìm Và Bài Tập

ĐĂNG KÝ NGAY

Các phép toán với số phức

Phép cộng

Để cộng hai số phức với nhau, ta cộng hai phần thực và hai phần ảo của chúng.

(a + bi) + (c + di) = (a + c) + (b + d)i

Phép trừ

Để trừ hai số phức với nhau, ta trừ hai phần thực và hai phần ảo của chúng.

(a + bi) - (c + di) = (a - c) + (b - d)i

Phép nhân

Để nhân hai số phức, các em nhân đa thức rồi thay phần biểu diễn số phức vào trong kết quả vừa nhận được.

(a +bi)(c + di) = (ac - bd) + (ad + bc)i

Phép chia

\begin{aligned} &\footnotesize \text{Phép chia hai số phức c + di và a + bi với nhau được thực hiện bằng cách }\\ &\footnotesize \text{nhân cả tử và mẫu với số phức liên hợp của a + bi.} \\ &\frac{c+di}{a+bi}=\frac{(c+di)(a-bi)}{a^2-b^2i^2}=\frac{ac+bd}{a^2+b^2}+\frac{ad-bc}{a^2+b^2}i \end{aligned}

Định nghĩa số phức nghịch đảo

Số phức nghịch đảo của số phức z có kí hiệu z-1. Tích của số phức ban đầu và số phức nghịch đảo của nó bằng 1.

z.z^{-1}=1

Chứng minh số phức nghịch đảo

Dễ \ dàng \ chứng \ minh \ z^{-1} =\frac{1}{|z|^2}.\overline{z}=\frac{1}{a^2+b^2}(a-bi) \\ \ \\ Suy \ ra: \ z^{-1}.z=\frac{1}{a^2+b^2}(a-bi)(a+bi)=\frac{a^2-b^2i^2}{a^2+b^2}=1 \\ \ \\ \bull \ Số \ phức \ dạng \ nghịch \ đảo \ của \ số \ phức \ z =a+bi \ là \ số \ phức \ z^{-1} =\frac{1}{z}=\frac{1}{a+bi} \\ \ \\ \bullet \ Số \ nghịch \ đảo \ của \ số \ phức \ z =a+bi \ khác \ 0 \ là \ số \ phức \ z^{-1} =\frac{1}{z}=\frac{\overline{z}}{|z|^2}

Một số ví dụ về số phức nghịch đảo

\bullet \ Số \ phức \ nghịch \ đảo \ của \ số \ phức \ z = 3 + 4i \ là \ \frac{3}{25}-\frac{4}{25}i \\ \ \\ \bullet \ Số \ phức \ nghịch \ đảo \ của \ số \ phức \ z = 1 + 3i \ là \ \frac{1}{10}-\frac{3}{10}i \\ \ \\ \bullet \ Số \ phức \ nghịch \ đảo \ của \ số \ phức \ z = 1 - 2i \ là \ \frac{1}{5}+\frac{2}{5}i

Cách tìm số phức nghịch đảo bằng máy tính cầm tay

Hiện nay, máy tính cầm tay được sử dụng phổ biến trong quá trình học của các em học sinh. Vì vậy, việc áp dụng máy tính để giải bài tập đã trở nên phổ biến. Cụ thể, để tìm số phức nghịch đảo bằng máy tính cầm tay, các em thực hiện các bước sau:

Số Phức Đối Là Gì? Cách Tìm Điểm Biểu Diễn Của Số Phức Đối

Ví dụ: Sử dụng máy tính cầm tay, các em hãy tìm số phức nghịch đảo của các số phức sau đây:

\begin{aligned} &a) \sqrt{2}-i\sqrt{3}\\ &b)\frac{1-1\sqrt{3}}{7+21} \end{aligned}

Lời giải:

Các em sử dụng máy tính Casio fx-570ES PLUS và thực hiện lần lượt các bước sau:

\begin{aligned} &\bull \footnotesize\text{Bước 1: Chọn chương trình số phức bằng cách bấm MODE 2.}\\ &\bull \footnotesize \text{Bước 2: Nhập vào màn hình máy tính biểu thức }(\sqrt{2}-i\sqrt{3})^{-1}\\ &\bull \footnotesize \text{Bước 3: Bấm phím “=” sẽ thu được kết quả là } \frac{\sqrt{2}}{5}+\frac{\sqrt{3}}{5}i\\ &\footnotesize \text{Vậy số phức nghịch đảo của }(\sqrt{2}-i\sqrt{3})^{-1} \ là \ \frac{\sqrt{2}}{5}+\frac{\sqrt{3}}{5}i\\ \end{aligned}

Tham khảo ngay các khoá học online của Marathon Education

Gia sư Online Học Online Toán 12 Học Online Hóa 10 Học Online Toán 11 Học Online Toán 6 Học Online Toán 10 Học Online Toán 7 Học Online Lý 10 Học Online Lý 9 Học Online Toán 8 Học Online Toán 9 Phương Trình Lượng Giác Thường Gặp - Lý Thuyết Toán 11 Học Tiếng Anh 6 Học Tiếng Anh 7

Bên cạnh việc học tập và vận dụng những kiến thức về số phức nghịch đảo mà Marathon Education chia sẻ trên đây, các em cũng nên rèn luyện kỹ năng giải bài tập thường xuyên tại nhà để giúp việc học toán trở nên dễ dàng hơn. Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học trực tuyến nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!