2005) Và (√2006 + √2005) Là Hai Số Nghịch đảo Của Nhau.cô Giáo ...

Đăng nhập K Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xác nhận câu hỏi phù hợp Mua vip

Hành động

• Cập nhật
• Xóa

Hành động

• Báo cáo
• Cập nhật
• Xóa

LT Lê Thảo Linh 18 tháng 7 2015

 Chứng minh. (√2006 - √2005) và (√2006 + √2005) là hai số nghịch đảo của nhau.cô giáo mình giải rồi:Ta có: (√2006 - √2005) . (√2006 + √2005)

= (√2006)^2 - (√2005)^2= 2006 - 2005 = 1 (đpcm) 

Nhưng mình không hiểu cái chỗ vì sao mà: (√2006 - √2005) . (√2006 + √2005)  lại = (√2006)^2 - (√2005)^2 được. 

#Hỏi cộng đồng OLM #Toán lớp 9 2

NL Nguyễn Lương Bảo Tiên 18 tháng 7 2015

Hằng đẳng thức a2 - b2 = (a - b).(a + b) <=> (a - b).(a + b) = a2 - b2

Đúng(0)

HN Hiền Nguyễn Thu 29 tháng 7 2018

bạn nên hỏi luôn khi cô giảng chứ, đừng giấu dốt nhé

Đúng(0) Xem thêm câu trả lời Các câu hỏi dưới đây có thể giống với câu hỏi trên PT Pham Trong Bach 23 tháng 8 2017  Chứng minh: a )   2 - 3 2 + 3 = 1 b ) 2006 - 2005   v à   2006 + ...Đọc tiếp

 Chứng minh:

a )   2 - 3 2 + 3 = 1 b ) 2006 - 2005   v à   2006 + 2005

là hai số nghịch đảo của nhau.

#Hỏi cộng đồng OLM #Toán lớp 9 1

CM Cao Minh Tâm 23 tháng 8 2017

(Ghi chú: Muốn chứng minh hai số là nghịch đảo của nhau, ta chứng minh tích của hai số bằng 1.)

Đúng(0) ND Nguyen Duc Hieu 27 tháng 7 2017

a) (2 - √3)(2 + √3) = 1;

b) (√2006 - √2005) và (√2006 + √2005) là hai số nghịch đảo của nhau.

#Hỏi cộng đồng OLM #Toán lớp 9 2

T thuongnguyen 27 tháng 7 2017

Ủa đề là j vậy bạn . @Nguyen Duc Hieu

Nếu là đề yêu cầu chứng minh ( vì trong sgk toán 9 có ) thì làm như sau :

Đề :

Chứng minh

a) (2 - √3)(2 + √3) = 1;

b) (√2006 - √2005) và (√2006 + √2005) là hai số nghịch đảo của nhau.

----------------------------------------------------------------------------------------------------------------------------------

a) \(\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=1\)

Ta biến đổi vế trái :

\(VT=\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=4+2\sqrt{3}-2\sqrt{3}-\sqrt{3^2}=4-3=1\)

b) \(\left(\sqrt{2006}-\sqrt{2005}\right)v\text{à}\left(\sqrt{2006}+\sqrt{2005}\right)\)

Ta có : Nếu : ( \(\sqrt{2006}-\sqrt{2005}\) )( \(\sqrt{2006}+\sqrt{2005}\) ) =1 thì (√2006 - √2005) và (√2006 + √2005) là hai số nghịch đảo của nhau. Đúng(0)

CB co be bo cap 27 tháng 7 2017

đề dễ vậy cậu có thể tự làm đc mà :)

Đúng(0) Xem thêm câu trả lời TL the leagendary history 5 tháng 9 2021

Chứng minh:

\(\left(\sqrt{2006}-\sqrt{2005}\right)\)và \(\left(\sqrt{2006}+\sqrt{2005}\right)\)là 2 số nghịch đảo của nhau.

#Hỏi cộng đồng OLM #Toán lớp 9 3

NH Nguyễn Hoàng Minh 5 tháng 9 2021

Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)

Ta có 

\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)

\(\RightarrowĐfcm\)

Đúng(6)

NT Nguyễn Thu Hòa Official 5 tháng 9 2021

Đúng(1) Xem thêm câu trả lời H hoc 10 tháng 6 2017

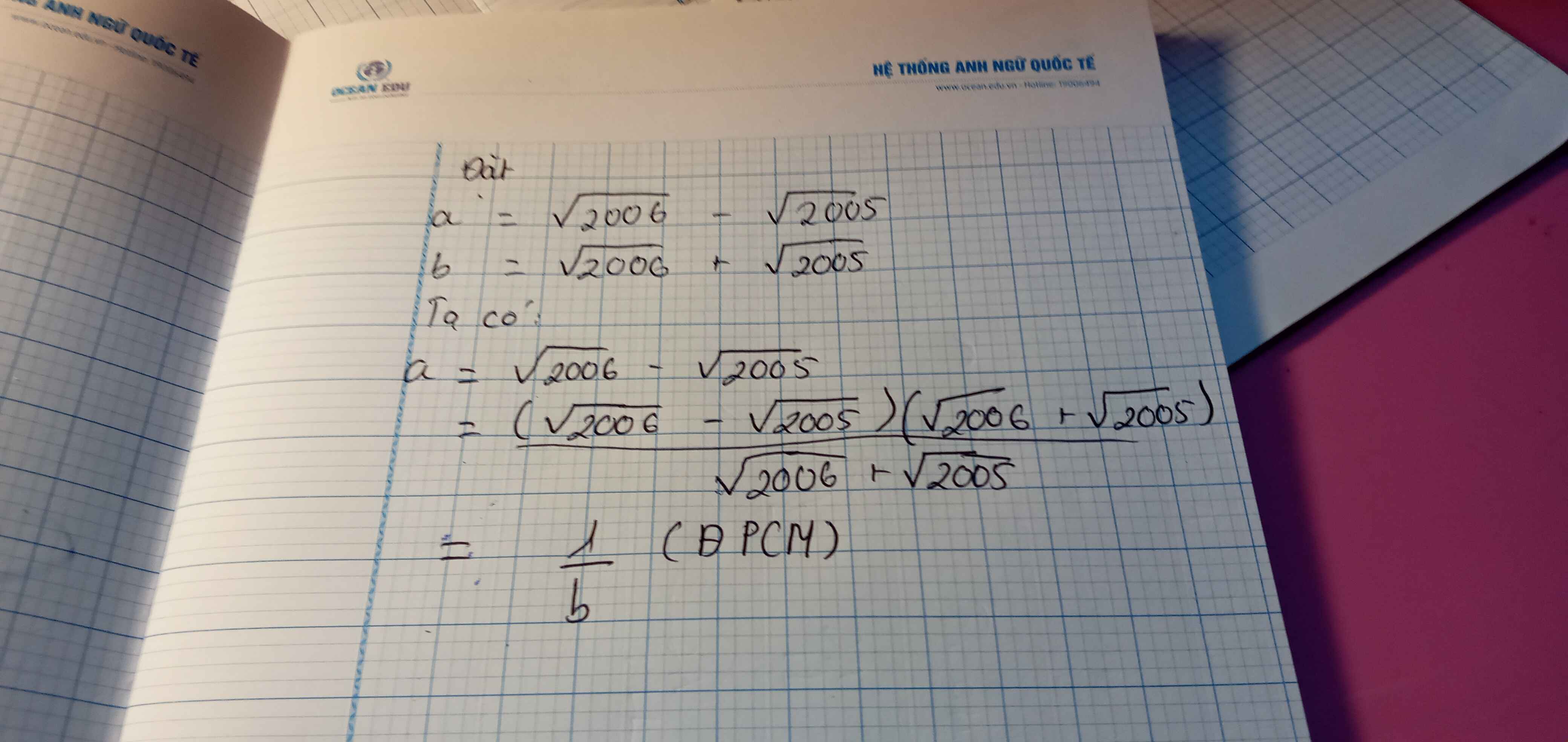
chứng minh \(\left(\sqrt{2006}-\sqrt{2005}\right)\)và\(\left(\sqrt{2006}+\sqrt{2005}\right)\)là hai số nghịch đảo của nhau

#Hỏi cộng đồng OLM #Toán lớp 9 2

N nghia 10 tháng 6 2017

\(\left(x-\sqrt{11}\right)^2=0\)

\(\left(x-\sqrt{11}\right)=0\)

\(x=\sqrt{11}\)

Đúng(0)

TV Thành viên 10 tháng 6 2017

\(\left(x-\sqrt{11}^2=0\right)\)

\(\left(x-\sqrt{11}\right)=0\)

\(x=\sqrt{11}\)

Đúng(0) Xem thêm câu trả lời NM Nguyễn Minh Thu 9 tháng 8 2016

Chứng minh rằng \(\left(\sqrt{2006}-\sqrt{2005}\right)\)và \(\left(\sqrt{2006}+\sqrt{2005}\right)\) là hai số nghịch đảo

#Hỏi cộng đồng OLM #Toán lớp 9 2

HL Hoàng Lê Bảo Ngọc 9 tháng 8 2016

Đặt \(a=\sqrt{2006}-\sqrt{2005}\) , \(b=\sqrt{2006}+\sqrt{2005}\)

Ta sẽ chứng minh \(a=\frac{1}{b}\)

Ta có : \(a=\sqrt{2006}-\sqrt{2005}=\frac{\left(\sqrt{2006}-\sqrt{2005}\right).\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\frac{2006-2005}{\sqrt{2006}+\sqrt{2005}}\)

\(=\frac{1}{\sqrt{2006}+\sqrt{2005}}=\frac{1}{b}\)

Vậy a và b là hai số nghịch đảo.

Đúng(0)

NT Ngô Tấn Trí 9 tháng 8 2016

Đầu tiên nhắc lại định nghĩ hai số nghịch đảo: Hai số được gọi là nghịch đảo nếu tích của chúng bằng 1.

Vd: $ab=1\implies $ a và b là hai số nghịch đảo của nhau và ngược lại nếu a và b  là hai số nghịch đảo của nhau thì $ab=1$.

Áp dụng vào bài toán trên ta có: $(\sqrt{2006}-\sqrt{2005})(\sqrt{2006}-\sqrt{2005})=1\implies $ hai số trên là nghịch đảo của nhau.

Đúng(0) Xem thêm câu trả lời HD Hoàng Đình Đại 21 tháng 10 2018

Tính

\(A=\sqrt{1+2005+\left(\frac{2005}{2006}\right)^2}+\frac{2005}{2006}\)

Các bạn giải hộ mình nhé ^_^

#Hỏi cộng đồng OLM #Toán lớp 9 0 HD Hoàng Đình Đại 21 tháng 10 2018

Tính

\(A=\sqrt{1+2005+\left(\frac{2005}{2006}\right)^2}+\frac{2005}{2006}\)

Các bạn giải hộ mình nhé ^_^

#Hỏi cộng đồng OLM #Toán lớp 9 0 DT Dũng Trịnh 11 tháng 9 2017

\(\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4}=\sqrt{1+2005^2+\dfrac{2005^2}{2006^2}+\dfrac{2005}{2006}}\)

#Hỏi cộng đồng OLM #Toán lớp 9 1

UK Unruly Kid 13 tháng 9 2017

Sửa đề:

\(VP=\sqrt{1+2005^2+\dfrac{2005^2}{2006^2}}+\dfrac{2005}{2006}\)

Ta có: \(2005^2+1=\left(2005+1\right)^2-2.2005.1=2006^2-2.2005\)

\(\Rightarrow VP=\sqrt{2006^2-2.2005+\dfrac{2005^2}{2006^2}}+\dfrac{2005}{2006}\)

\(=\sqrt{\left(2006-\dfrac{2005}{2006}\right)^2}+\dfrac{2005}{2006}\)

\(=2006-\dfrac{2005}{2006}+\dfrac{2005}{2006}=2006\)

Phương trình đã cho tương đương

\(\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4}=2006\)

\(\Leftrightarrow\sqrt{\left(x-1\right)^2}+\sqrt{\left(x-2\right)^2}=2006\)

\(\Leftrightarrow\left|x-1\right|+\left|x-2\right|=2006\)

Đến đây thì tự xét trường hợp và giải tìm nghiệm, bài này không cần điều kiện nhé

Đúng(0) LM Lâm Minh Anh 20 tháng 10 2016

giải phương trình  | x-2005 | ^ 2005 +  | x - 2006 | ^ 2006=1

#Hỏi cộng đồng OLM #Toán lớp 9 1

N ngonhuminh 21 tháng 10 2016

x-2006=y

I(y+1)I^2005+IyI^2006=1 

=> y=0, y=-1

x=2006 hoac x=2005

Đúng(0) Đăng nhập

• Trang chủ
• Học bài
• Hỏi đáp
• Kiểm tra
• Trợ giúp
• Bài viết
  • Tin tức
  • Cuộc thi

Hãy đăng nhập để tiếp tục sử dụng OLM

Tên đăng nhập Mật khẩu Ghi nhớ đăng nhập Quên mật khẩu? Đăng nhập Chưa có tài khoản? Mã xác thực Tiếp tục Để sau Đăng ký

Các khóa học có thể bạn quan tâm

Mua khóa học Tổng thanh toán: 0đ (Tiết kiệm: 0đ) Tới giỏ hàng Đóng ×

Yêu cầu VIP

Học liệu này đang bị hạn chế, chỉ dành cho tài khoản VIP cá nhân, vui lòng nhấn vào đây để nâng cấp tài khoản.

Không Có

Yêu cầu đăng nhập

Bạn phải đăng nhập để thực hiện hành động này:

Đăng nhập Hoặc Đăng ký

Cảnh báo

Đóng