Chứng Minh Rằng Tổng Của Một Phân Số Dương Với Số ... - Hoc24

HOC24

Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng

• Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn

Đóng Đăng nhập Đăng ký

Lớp học

• Lớp 12
• Lớp 11
• Lớp 10
• Lớp 9
• Lớp 8
• Lớp 7
• Lớp 6
• Lớp 5
• Lớp 4
• Lớp 3
• Lớp 2
• Lớp 1

Môn học

• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Đạo đức
• Tự nhiên và xã hội
• Khoa học
• Lịch sử và Địa lý
• Tiếng việt
• Khoa học tự nhiên
• Hoạt động trải nghiệm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Chủ đề / Chương

Bài học

HOC24

Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng

• Tất cả
• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Hãy tham gia nhóm Học sinh Hoc24OLM Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài

Câu hỏi

Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay

• Pham Trong Bach

2 tháng 9 2019 lúc 13:45

Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2.

Xem chi tiết Lớp 6 Toán 1 0 Gửi Hủy Cao Minh Tâm 2 tháng 9 2019 lúc 13:46

Gọi a/b với a > 0, b > 0 là phân số đã cho và b/a là phân số nghịch đảo của nó . Không mất tính tổng quát giả sử 0 < a ≤ b.

Đặt b = a + m (m ∈ Z, m ≥ 0)

Ta có:

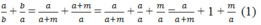
Và 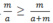 (dấu "=" xảy ra khi m = 0)

Suy ra: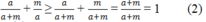 

Từ (1) và (2) suy ra:

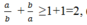, (dấu "=" xảy ra khi m = 0 hay a = b )

Đúng 0 Bình luận (0) Gửi Hủy

• Ngô Thành Vinh

2 tháng 3 2017 lúc 5:34

Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2

Xem chi tiết Lớp 6 Toán Câu hỏi của OLM 1 0 Gửi Hủy Pham Thuy Linh 2 tháng 3 2017 lúc 5:59

Giả sử phân số và nghịch đảo của nó là: \(\frac{a}{b};\frac{b}{a}\)

Do phân số dương nên( a;b) cùng dấu hay a.b>0

Ta có:

\(\frac{a}{b}+\frac{b}{a}-2=\frac{a^2+b^2-2ab}{ab}=\frac{\left(a-b\right)^2}{ab}\ge0\)

Do đó: \(\frac{a}{b}+\frac{b}{a}\ge2\)

Đúng 0 Bình luận (0) Gửi Hủy

• Bài 101*

Sách bài tập - tập 2 - trang 29 15 tháng 5 2017 lúc 21:12

Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2 ?

Xem chi tiết Lớp 6 Toán Bài 12: Phép chia phân số 2 0 Gửi Hủy Hàn Thất Lục 15 tháng 5 2017 lúc 21:22

Gọi phân số dương là \(\dfrac{a}{b}\) . ( Không mất tính tổng quát )

Cho \(a>0,\) \(b>0\) và \(a\ge b\) . Ta có thể viết \(a=b+m\left(m\ge0\right)\) .

Ta có:

\(\dfrac{a}{b}+\dfrac{b}{a}=\dfrac{b+m}{b}+\dfrac{b}{b+m}=1+\dfrac{m}{b}\ge1+\dfrac{m}{b+m}+\dfrac{b}{b+m}=1+\dfrac{m+b}{b+m}=2\)\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{a}\ge2\)

Dấu đẳng thức xảy ra khi \(a=b\left(m=0\right)\)

Đúng 0 Bình luận (0) Gửi Hủy Hải Đăng 1 tháng 5 2018 lúc 17:53

Gọi a/b với a > 0, b > 0 là phân số đã cho và b/a là phân số nghịch đảo của nó . Không mất tính tổng quát giả sử 0 < a ≤ b.

Đặt b = a + m (m ∈ Z, m ≥ 0)

Ta có:

Và 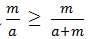(dấu "=" xảy ra khi m = 0)

Suy ra:

Từ (1) và (2) suy ra:

, (dấu "=" xảy ra khi m = 0 hay a = b )

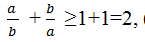
Đúng 0 Bình luận (0) Gửi Hủy

• Chu Kim Ngân

14 tháng 3 2016 lúc 19:55

chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2?

  Xem chi tiết Lớp 0 Toán 3 0 Gửi Hủy Lê Minh Đức 14 tháng 3 2016 lúc 20:29

 Gọi phân số đó là a/b (ĐK: a,b # 0, a và b cùng dấu ) a/b + b/a ≥ 2 <=> (a² + b ²)/ab ≥ 2 <=> a² - 2ab + b² ≥ 0 <=> ( a – b )² ≥ 0 ( Luôn đúng với mọi a, b) => Đpcm  

Đúng 0 Bình luận (2) Gửi Hủy Lê Anh Thư 19 tháng 8 2016 lúc 16:50

mk giải đc nè, tick mk nha!!

Gọi phân số  dương là a/b. Ko mất tính tổng quát, giả sử như: a>0, b>0 và a  > b. Ta có thể viết a=b+m ( m > 0). Ta có:

a/b+b/a=b+m/b+b/m+b=1+m/b+b/b+m >  1+ m/b+m+b/b+m=1+m+b/b+m=2.

Vậy a/b+b/a > 2.

 

Đúng 0 Bình luận (2) Gửi Hủy Nguyễn Lưu Vũ Quang 25 tháng 3 2017 lúc 20:31

Gọi phân số dương là a/b. Không mất tính tổng quát, giả sử a>0, b>0 và a\(\ge\)b. Ta có thể viết a=b+m (m\(\ge\)0). Ta có:

(a/b)+(b/a)=b/(b+m)\(\ge\)1+[m/(b+m)]+[b/(b+m)]=1+[(m+b)/(b+m)]=2.

Vậy (a/b)+(b/a)=2

Dấu đẳng thức xảy ra khi a=b (m=0).

Đúng 0 Bình luận (0) Gửi Hủy

• Minh Thư

2 tháng 4 2015 lúc 20:32

Bài toán: Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2

Xem chi tiết Lớp 6 Toán Câu hỏi của OLM 4 0 Gửi Hủy Tony Tony Chopper 14 tháng 3 2017 lúc 20:58

nói thật thì đó là toán lớp 8, lớp 9 chứ k phải lớp 6

gọi phân số đó là a/b, vì phân số dương => a.b dương. Ta phải đi chứng minh a/b+b/a lớn hơn hoặc bằng 2

\(\frac{a}{b}+\frac{b}{a}=\frac{a^2+b^2}{ab}=\frac{a^2-ab-ab+b^2}{ab}+2=\frac{a\left(a-b\right)-b\left(a-b\right)}{ab}+2\)

\(=\frac{\left(a-b\right)^2}{ab}+2\ge2\)(vì (a-b)^2 lớn hơn hoặc bằng 0 và ab>0 => phân số đầu tiên không âm, suy ra tổng không nhỏ hơn 2)

Đúng 0 Bình luận (0) Gửi Hủy ɱ√ρ︵★bĭ ¢ồ★ ღиɢυуễи⁀ᶦᵈᵒ... 20 tháng 3 2019 lúc 20:03

Ai chs opoke đại chiên lh mik nha! Đỏi lấy nick olm hoặc cho mik

Đúng 0 Bình luận (0) Gửi Hủy Đặng thế thiện 26 tháng 3 2019 lúc 21:28

đọc chưa hiểu ?!!!!.....?

Đúng 0 Bình luận (0) Gửi Hủy Xem thêm câu trả lời

• Nguyễn Thị Thùy Trang

10 tháng 6 2015 lúc 7:33

chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn hai ?

Xem chi tiết Lớp 6 Toán Câu hỏi của OLM 3 0 Gửi Hủy Mr Lazy 10 tháng 6 2015 lúc 12:07

Giả sử phân số và nghịch đảo của nó là \(\frac{a}{b};\frac{b}{a}\)

Do phân số dương nên \(a;b\)cùng dấu hay \(a.b>0\)

Ta có \(\frac{a}{b}+\frac{b}{a}-2=\frac{a^2+b^2-2ab}{ab}=\frac{\left(a-b\right)^2}{ab}\ge0\)

Do đó \(\frac{a}{b}+\frac{b}{a}\ge2\)

Đúng 0 Bình luận (0) Gửi Hủy yuki asuna 15 tháng 2 2018 lúc 15:30

Đúng rùi

Đúng 0 Bình luận (0) Gửi Hủy Đỗ Vũ Bá Linh 21 tháng 6 2021 lúc 16:43

Gọi phân số dương là \(\frac{a_1}{a_2}\). Không mất tính tổng quát, giả sử \(a_1\ge a_2>0\). Ta có thể viết \(a_1=a_2+m\)\(\left(m\inℕ\right)\). Ta có:\(\frac{a_1}{a_2}+\frac{a_2}{a_1}=\frac{a_2+m}{a_2}+\frac{a_2}{a_2+m}=1+\frac{m}{a_2}+\frac{a_2}{a_2+m}\ge1+\frac{m}{a_2+m}+\frac{a_2}{a_2+m}=1+\frac{m+a_2}{a_2+m}=2\)Vậy \(\frac{a_1}{a_2}+\frac{a_2}{a_1}\ge2\).Dấu đẳng thức xảy ra khi \(a_1=a_2\)\(\left(m=0\right)\).

Đúng 0 Bình luận (0) Khách vãng lai đã xóa Gửi Hủy

• Nguyễn Ngọc Tú Trân

13 tháng 3 2018 lúc 18:37

Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2.

 

Xem chi tiết Lớp 6 Toán Câu hỏi của OLM 1 0 Gửi Hủy bin 22 tháng 3 2019 lúc 8:17

Ta gọi phân số đó là \(\frac{a}{b}\) ,vì phân số dương\(\Rightarrow a.b=\)dương .

Ta chúng minh \(\frac{a}{b}+\frac{b}{a}\ge2\)

\(\frac{a}{b}+\frac{b}{a}=\frac{a^2+b^2}{ab}=\frac{a^2-ab-ab+b^2}{ab}+2=\frac{a\left(a-b\right)-b\left(a-b\right)+2}{ab}\)

\(=\frac{\left(a-b\right)^2}{ab}+2\ge2\)

Vì :

\(\left(a-b\right)^2\ge0\) và \(ab>0\)

\(\Rightarrow\)Phân số không âm .

\(\Rightarrow\)Tổng không bé hơn 2

Đúng 0 Bình luận (0) Gửi Hủy

• Tuananh Vu

4 tháng 4 2016 lúc 18:33

Bài 101*:

Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2

Xem chi tiết Lớp 6 Toán Câu hỏi của OLM 0 0 Gửi Hủy

• Tạ Thu Anh

26 tháng 3 2016 lúc 20:24

a)Chứng minh rằng tổng của một phân số dương với nghịch đảo của nó không nhỏ hơn 2.

b) Tìm các phân số có tử và mẫu đều dương sao cho tổng của phân số đó với nghịch đảo của nó có giá trị nhỏ nhất.

Xem chi tiết Lớp 6 Toán Câu hỏi của OLM 1 0 Gửi Hủy Tạ Thu Anh 26 tháng 3 2016 lúc 20:38

a. Gọi phân số cần tìm là \(\frac{a}{b}\)

\(\Rightarrow\) Phân số nghịch đảo là \(\frac{b}{a}\)

Theo bài ra, ta có:

\(\frac{a}{b}+\frac{b}{a}\ge2\)

\(\Leftrightarrow\frac{a^2+b^2}{ab}\ge2\)

\(\Leftrightarrow a^2+b^2\ge2ab\)

\(\Leftrightarrow a^2+b^2-2ab\ge0\)

\(\Leftrightarrow a^2-ab+b^2-ab\ge0\)

\(\Leftrightarrow a\left(a-b\right)+b\left(b-a\right)\ge0\)

\(\Leftrightarrow a\left(a-b\right)-b\left(a-b\right)\ge0\)

\(\Leftrightarrow\left(a-b\right)\left(a-b\right)\ge0\)

\(\Leftrightarrow\left(a-b\right)^2\ge0\)

Vì (a-b)2 chắc chắn lớn hơn hoặc bằng 0

\(\Rightarrow\frac{a}{b}+\frac{b}{a}\ge2\)

                                Vậy tổng của một phân số dương với ghịch đảo của nó luôn lớn hơn hoặc bằng 2.

Đúng 0 Bình luận (0) Gửi Hủy

• Quản gia Whisper

15 tháng 4 2016 lúc 20:52

Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó không nhỏ hơn 2

Xem chi tiết Lớp 6 Toán Câu hỏi của OLM 6 0 Gửi Hủy Hoàng Phúc 15 tháng 4 2016 lúc 20:47

gọi p/s đó là a/b (a;b \(\in\) Z,b \(\ne\) 0)

Ta cần c/m \(\frac{a}{b}+\frac{b}{a}\ge2\)

Nhân cả 2 vế cho ab,ta đc:

\(\left(\frac{a}{b}+\frac{b}{a}\right).ab\ge2ab\)

\(\Leftrightarrow\frac{a^2b}{b}+\frac{b^2a}{a}\ge2ab\Leftrightarrow a^2+b^2\ge2ab\)

\(\Leftrightarrow a^2+b^2-2ab\ge0\Leftrightarrow\left(a-b\right)^2\ge0\) (dấu "=" xảy ra <=>a=b0

BĐT cuối luôn đúng,ta có đpcm

Đúng 0 Bình luận (0) Gửi Hủy Quản gia Whisper 15 tháng 4 2016 lúc 20:40

Gọi phân số dương là \(\frac{a}{b}\).Không mất tích tổng quát giả sử a>0,b>0 và a\(\ge\) b.Ta có thể viết a=b+m(m\(\ge\) 0).Ta có;

\(\frac{a}{b}+\frac{b}{a}=\frac{b+m}{b}+\frac{b}{m+b}\)

=\(1+\frac{m}{b}+\frac{b}{m+b}\ge1+\frac{m}{b+m}+\frac{b}{b+m}\)

=\(1+\frac{m+b}{b+m}=2\)

Vậy \(\frac{a}{b}+\frac{b}{a}\ge2\)

Đúng 0 Bình luận (0) Gửi Hủy zZz Phan Cả Phát zZz 15 tháng 4 2016 lúc 20:41

Gọi p/s đó là : a/b ( vs mọi a:b \(\in\) N* ) 

Theo bài ra ta có : 

a/b + b/a = \(\frac{2a+2b}{ab}\) = \(\frac{2\left(a+b\right)}{ab}\)

Vậy  tổng của một phân số dương với số nghịch đảo của nó không nhỏ hơn 2

Đúng 0 Bình luận (0) Gửi Hủy Xem thêm câu trả lời